function VBR = CB_003_JF10()
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% CB_003_JF10.m
%
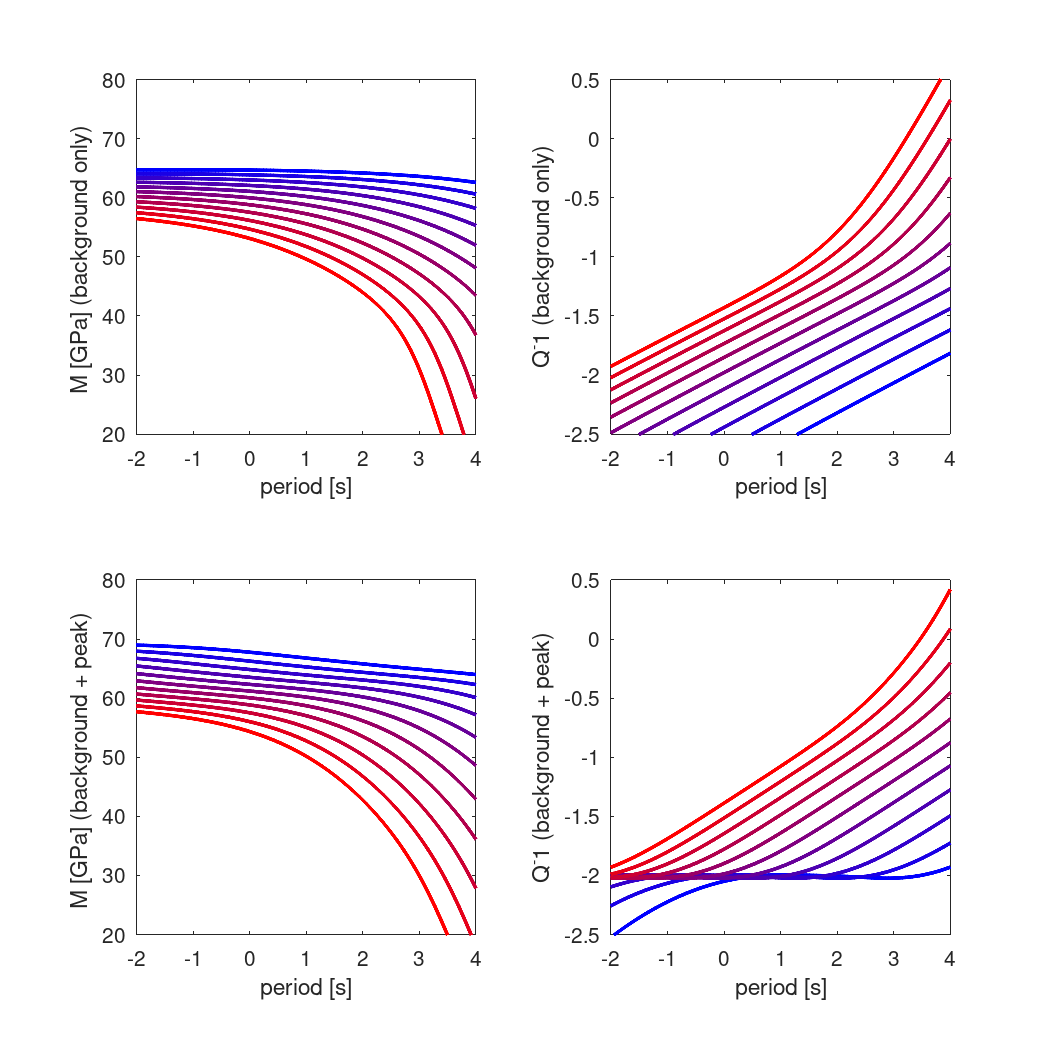
% Reproduces figures 1a-1d from JF10: moduli and Qinv vs period for
% a single sample, sample 6585, using coefficients for the single sample fit
% in table 1 of JF10.
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% write method list %%
VBR.in.elastic.methods_list={'anharmonic'};
VBR.in.anelastic.methods_list={'eburgers_psp';'andrade_psp'};
%% load anharmonic parameters, adjust Gu_0_ol %%
% all params in ../vbr/vbrCore/params/ will be loaded in call to VBR spine,
% but you can load them here and adjust any one of them (rather than changing
% those parameter files).
VBR.in.elastic.anharmonic=Params_Elastic('anharmonic'); % unrelaxed elasticity
VBR.in.anelastic.eburgers_psp=Params_Anelastic('eburgers_psp');
% use the single sample background only fit:
VBR.in.anelastic.eburgers_psp.eBurgerMethod='s6585_bg_only'; % 'bg_only' or 'bg_peak' or 's6585_bg_only'
% JF10 have Gu_0=62.5 GPa, but that's at 900 Kelvin and 0.2 GPa,
% so set Gu_0_ol s.t. it ends up at 62.5 at those conditions
dGdT=VBR.in.elastic.anharmonic.isaak.dG_dT;
dGdP=VBR.in.elastic.anharmonic.cammarano.dG_dP;
Tref=VBR.in.elastic.anharmonic.T_K_ref;
Pref=VBR.in.elastic.anharmonic.P_Pa_ref/1e9;
GUJF10=VBR.in.anelastic.eburgers_psp.s6585_bg_only.G_UR;
VBR.in.elastic.anharmonic.Gu_0_ol = GUJF10 - (900+273-Tref) * dGdT/1e9 - (0.2-Pref)*dGdP; % olivine reference shear modulus [GPa]
% frequencies to calculate at
VBR.in.SV.f = 1./logspace(-2,4,100);
%% Define the Thermodynamic State %%
VBR.in.SV.T_K=700:50:1200;
VBR.in.SV.T_K=VBR.in.SV.T_K+273;
sz=size(VBR.in.SV.T_K); % temperature [K]
% remaining state variables
VBR.in.SV.dg_um=3.1*ones(sz);
VBR.in.SV.P_GPa = 0.2 * ones(sz); % pressure [GPa]
VBR.in.SV.rho = 3300 * ones(sz); % density [kg m^-3]
VBR.in.SV.sig_MPa = 10 * ones(sz); % differential stress [MPa]
VBR.in.SV.phi = 0.0 * ones(sz); % melt fraction
%% call VBR_spine %%
[VBR] = VBR_spine(VBR) ;
%% adjust VBR input to include dissipation peak in the eburgers method %%
VBR.in.anelastic.eburgers_psp.eBurgerFit='s6585_bg_peak';
% this fit has a slightly different ref modulus, adjust it again:
GUJF10=VBR.in.anelastic.eburgers_psp.s6585_bg_peak.G_UR;
VBR.in.elastic.anharmonic.Gu_0_ol = GUJF10 - (900+273-Tref) * dGdT/1e9 - (0.2-Pref)*dGdP;
%% Call VBR_spine again %%
[VBR_with_peak] = VBR_spine(VBR) ;
%% build figure %%
if ~vbr_tests_are_running()
figure('PaperPosition',[0,0,7,7],'PaperPositionMode','manual');
for iTemp = 1:numel(VBR.in.SV.T_K)
M_bg=squeeze(VBR.out.anelastic.eburgers_psp.M(1,iTemp,:)/1e9);
M_bg_peak=squeeze(VBR_with_peak.out.anelastic.eburgers_psp.M(1,iTemp,:)/1e9);
Q_bg=squeeze(VBR.out.anelastic.eburgers_psp.Qinv(1,iTemp,:));
Q_bg_peak=squeeze(VBR_with_peak.out.anelastic.eburgers_psp.Qinv(1,iTemp,:));
logper=log10(1./VBR.in.SV.f);
R=(iTemp-1) / (numel(VBR.in.SV.T_K)-1);
B=1 - (iTemp-1) / (numel(VBR.in.SV.T_K)-1);
subplot(2,2,1)
hold on
plot(logper,M_bg,'color',[R,0,B],'LineWidth',2);
ylabel('M [GPa] (background only) '); xlabel('period [s]')
ylim([20,80])
subplot(2,2,2)
hold on
plot(logper,log10(Q_bg),'color',[R,0,B],'LineWidth',2);
ylabel('Q^-1 (background only)'); xlabel('period [s]')
ylim([-2.5,0.5])
subplot(2,2,3)
hold on
plot(logper,M_bg_peak,'color',[R,0,B],'LineWidth',2);
ylabel('M [GPa] (background + peak) '); xlabel('period [s]')
ylim([20,80])
subplot(2,2,4)
hold on
plot(logper,log10(Q_bg_peak),'color',[R,0,B],'LineWidth',2);
ylabel('Q^-1 (background + peak)'); xlabel('period [s]')
ylim([-2.5,0.5])
end
for ip = 1:4
subplot(2,2,ip); box on;
end
saveas(gcf,'./figures/CB_003_JF10.png')
end
end