CB_012_simplecrust.m

output figures

'CB_012_simplecrust'
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% CB_012_simplecrust.m
%
%  Calculate seismic properties for steady state plate model with simple crust
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

%% put VBR in the path %%
  clear
  path_to_top_level_vbr='../../';
  addpath(path_to_top_level_vbr)
  vbr_init

%% Set Thermodynamic State Using Steady State Plate Model with no radiogenic heating %%
  % plate model
  Tsurf_C=0; % surface temperature [C]
  Tasth_C=1450; % asthenosphere temperature [C]
  zLAB=100; % lithosphere asthenosphere boundary [km]
  z_km=linspace(0,200,50)'; % depth, opposite vector orientation [km]
  dTdz_ad=0.3; % asthenosphere adiabat [C/km]
  rho_c=2800; % crustal density [kg/m3]
  drho=500; % crust-mantle density difference [kg/m3], rho_m=rho_c+drho
  z_moho=30; % moho depth [km]

  % linear geotherm to zLAB, adiabat below:
  T=(Tasth_C-Tsurf_C)*z_km/zLAB;
  T(z_km>zLAB)=Tasth_C+(z_km(z_km>zLAB)-zLAB)*dTdz_ad;

  % compositional factor, 0 for crust, 1 for olivine/mantle
  chi=ones(size(T));
  chi(z_km<=z_moho)=0;

  rho = rho_c * ones(size(T));
  rho(z_km>z_moho)= rho(z_km>z_moho) + drho;
  Psurf=0.2; % surface pressure, GPa
  P=cumtrapz(rho)*(z_km(2)-z_km(1))*1e3*9.8+Psurf*1e9;

%% Load and set VBR parameters %%
  VBR.in.elastic.methods_list={'anharmonic'};
  VBR.in.viscous.methods_list={'HK2003'};
  VBR.in.anelastic.methods_list={'andrade_psp';'xfit_mxw'};
  VBR.in.elastic.anharmonic=Params_Elastic('anharmonic'); % unrelaxed elasticity
  VBR.in.elastic.anharmonic.Gu_0_ol = 75.5; % olivine reference shear modulus [GPa]
  VBR.in.SV.f = [0.1];%  frequencies to calculate at

% copy model into VBR state variables, adjust units as needed
  VBR.in.SV.T_K = T+273; % temperature [K]
  VBR.in.SV.P_GPa = P/1e9; % pressure [GPa]
  VBR.in.SV.rho = rho; % density [kg m^-3]
  VBR.in.SV.chi = chi; % 0 for crust, 1 for olivine/mantle

  % set the other state variables as matrices of same size
  sz=size(T);
  VBR.in.SV.sig_MPa = 10 * ones(sz); % differential stress [MPa]
  VBR.in.SV.phi = 0.0 * ones(sz); % melt fraction
  VBR.in.SV.dg_um = 0.01 * 1e6 * ones(sz); % grain size [um]

%% CALL THE VBR CALCULATOR %%

%% first full anelasticity
  [VBR] = VBR_spine(VBR) ;

%% build figures
  figure('PaperPosition',[0,0,10,4],'PaperPositionMode','manual')
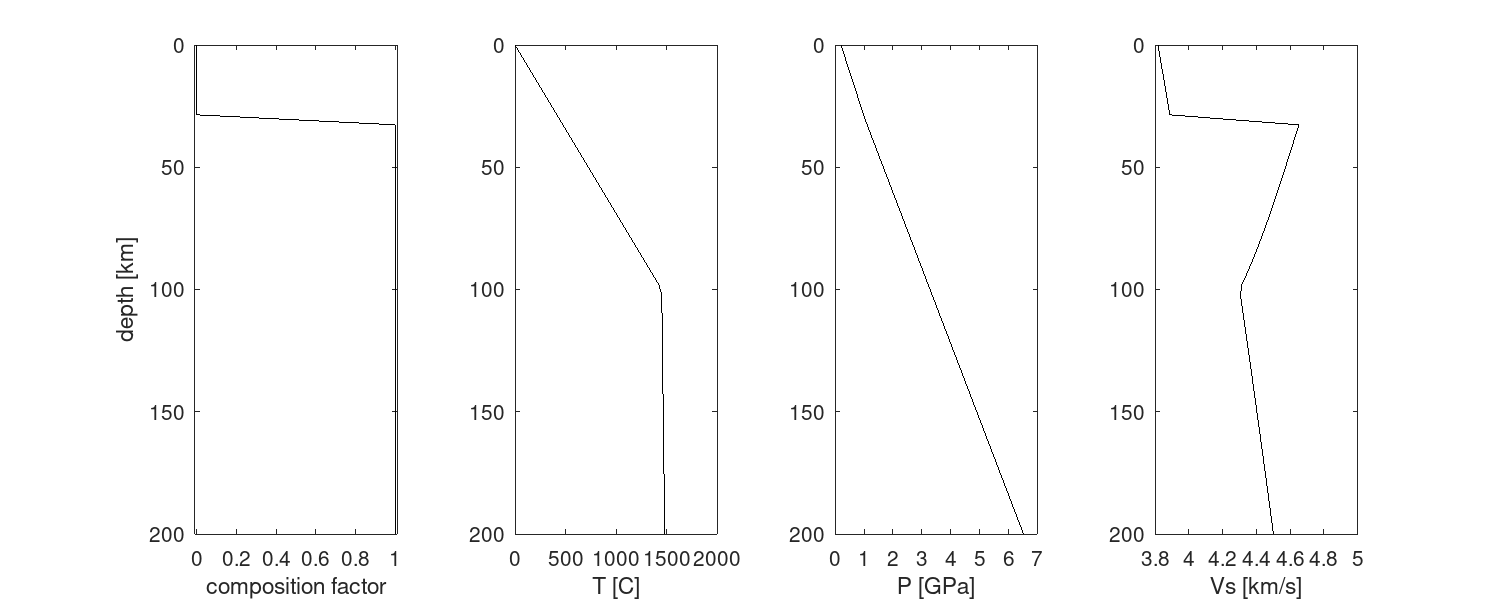
  subplot(1,4,4)
  plot(VBR.out.anelastic.andrade_psp.Vave/1e3,z_km,'k')
  xlabel('Vs [km/s]')
  set(gca,'ydir','reverse')
  subplot(1,4,2)
  plot(VBR.in.SV.T_K-273,z_km,'k')
  xlabel('T [C]')
  set(gca,'ydir','reverse')
  subplot(1,4,3)
  plot(VBR.in.SV.P_GPa,z_km,'k')
  xlabel('P [GPa]')
  set(gca,'ydir','reverse')
  subplot(1,4,1)
  plot(VBR.in.SV.chi,z_km,'k')
  ylabel('depth [km]')
  xlabel('composition factor')
  xlim([-.01,1.01])
  set(gca,'ydir','reverse')
  saveas(gcf,'./figures/CB_012_simplecrust.png')
CB_012_simplecrust.m

output figures

contents
