CB_022_backstress_maxwell.m

output figures

contents

function VBR = CB_022_backstress_maxwell
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    % CB_022_backstress_maxwell
    %
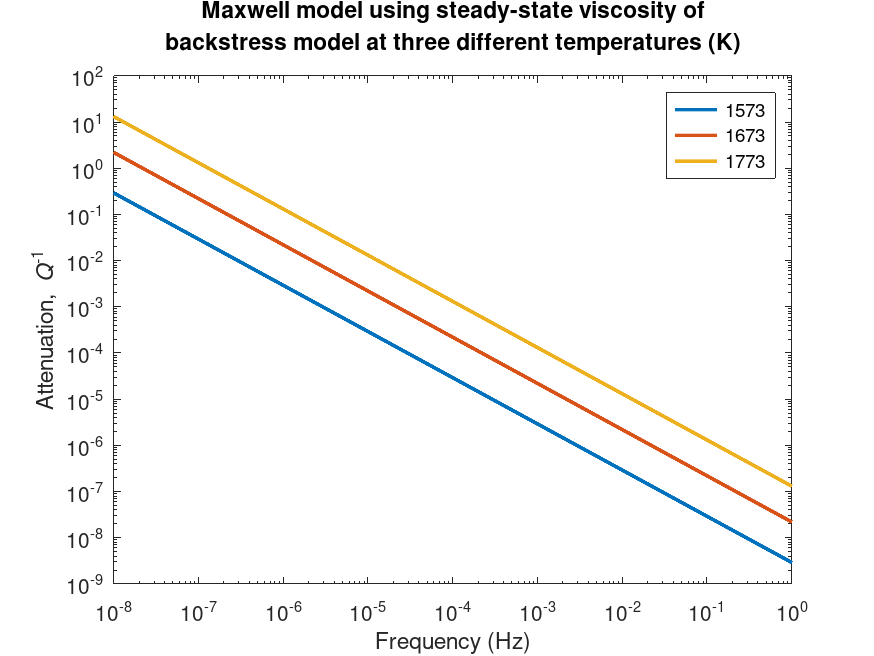
    % Demonstration of a Maxwell model with steady-state viscosity
    % of the backstress model using the analytical_maxwell model
    %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
    
    VBR.in.elastic.methods_list={'anharmonic';};
    VBR.in.viscous.methods_list={'BKHK2023'};
    VBR.in.anelastic.methods_list={'maxwell_analytical'};
    VBR.in.anelastic.maxwell_analytical.viscosity_method_mechanism = 'gbnp'; % select viscous method, in this case the backstress model with dislocation recovery by grain-boundary and pipe diffusion
    
    % set state variables
    VBR.in.SV.T_K = [1300, 1400, 1500] + 273;
    sz = size(VBR.in.SV.T_K);
    VBR.in.SV.sig_MPa = full_nd(3., sz);
    VBR.in.SV.dg_um = full_nd(10000, sz);

    % following are needed for anharmonic calculation
    VBR.in.SV.P_GPa = full_nd(5., sz);
    VBR.in.SV.rho = full_nd(3300, sz);
    VBR.in.SV.f = logspace(-8, 0, 500);%[0.001, 0.01]; 
    
    % calculations
    VBR = VBR_spine(VBR); % run VBR       
    
    % plotting
    if ~vbr_tests_are_running()
        loglog(VBR.in.SV.f,squeeze(VBR.out.anelastic.maxwell_analytical.Qinv),'LineWidth',2)
        title({'Maxwell model using steady-state viscosity of', 'backstress model at three different temperatures (K)'})
        xlabel('Frequency (Hz)')
        ylabel('Attenuation, {\it Q}^{-1}')
        legend([num2str(VBR.in.SV.T_K(1,:,1)')])
        box on
        saveas(gcf,'./figures/CB_022_backstress_maxwell.png')
    end        
end